亚波长超散射工程通过结合共振模式
${}^1$School of Physics, Harbin Institute of Technology, Harbin 150001, People’s Republic of China
${}^2$Heilongjiang Provincial Key Laboratory of Plasma Physics and Application Technology, Harbin 150001, People’s Republic of China
${}^3$Heilongjiang Provincial Innovation Research Center for Plasma Physics and Application Technology, Harbin 150001, People’s Republic of China
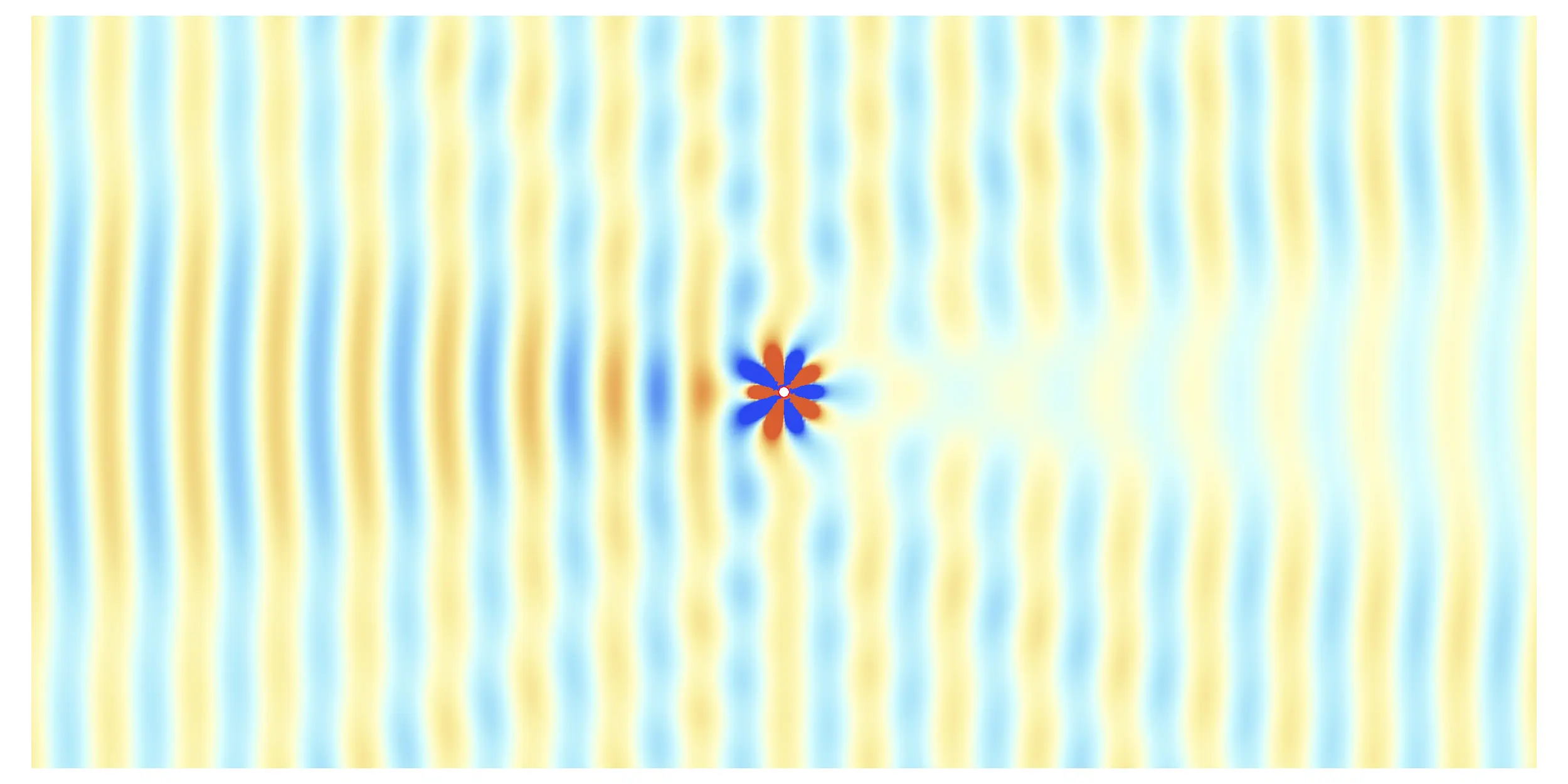 平面波射入一个具有强后向散射的超散射体
平面波射入一个具有强后向散射的超散射体引言
光与小颗粒的散射是现代光学中的一个基本问题,可以追溯到瑞利的工作 ( Rayleigh, 1871; Rayleigh, 1871)。光与物质相互作用的强度通常由散射截面来表征。在长波极限下,小颗粒对电磁波响应较弱,其散射截面与波长 $\lambda$ 的四次方成正比 ( Jackson, 1999)。因此,期望增强光与物质的相互作用以满足各种亚波长光子应用的需求,例如成像、传感、热传输等。幸运的是,在共振散射发生时,一个小物体可以产生远超瑞利散射的光学响应。这意味着它会表现出一个总散射截面不超出单通道限制。对于一个总散射截面超过单通道限制的小波长颗粒,称之为超散射体 ( Ruan, et al., 2010; Ruan, et al., 2011),暗示更强的光-物质耦合,并且由于其巨大的控制光能力而引起了极大的关注。
超散射工程在设计粒子结构时优化最大散射截面,同时保持能量守恒和中心对称性,已经实现在微波 ( Qian, et al., 2019), 声波 ( Lee, et al., 2019) 和 水波等系统中的各种应用。然而,超散射的发展侧重于增加总散射截面而忽略了其他散射特性。最近提出了多种结构的超散射体 ( Mirzaei, et al., 2014; Kumar, et al., 2020; Qian, et al., 2019; Qian, et al., 2018),但大多数都是以轻微或无后向散射构建而成,在其显著前向散射的对比下显得突兀。主要证明了超散射体保护其后的物体免受散射的能力。
后向散射是用于表征电磁性质的对象的重要特性,并特别关注于天线、雷达、通信、传感等领域 ( Wang, et al., 2021; Feng, et al., 2018; Hao, et al., 2023)。已经设计了多种具有强角度无关后向散射能力的反向反射结构,如角反射器、Luneberg 漫游者和超表面 ( Díaz-Rubio, et al., 2017; Arbabi, et al., 2017),这些结构被用于各种应用中,如不同领域的雷达目标或通信天线。然而,这些结构通常具有过长的波长轮廓且无法在亚波长范围内工作。因此,基于超散射机制开发一种亚波长反向反射器将为实现灵活散射特性工程及高灵敏度传感开辟道路。
通过设计散射体实现强后向散射已经在最近的研究中被讨论。例如,介电壳结构用于增强背向散射,在一些先前的工作中是通过结合一个电和磁场偶极子共振来实现的 ( Liberal, et al., 2015; Powell, et al., 2021; Powell, et al., 2022)。然而,这种方法局限于两个模式的组合,并在二维情况下失败。
在这项工作中,我们重新审视了2D旋转对称超散射系统中的这种被忽视的现象,并发现这种不寻常的行为可以归因于相邻角动量通道中共振模式的叠加。在这个过程中,我们概述了一般性视角,即前向和后向散射与模式组合之间的固有关系,并确认所设计的超散射体具有简化的后向散射特性。我们表明,根据正确重叠模式的数量,后向散射可以以平方形式增强,并且当给定数量的共振模式时,后向散射被最大化。原则上,通过特定设计的超散射体,任意大的后向散射可以实现。具体而言,我们将展示通过将三个非相邻共振模式组合在一个简单模型中实现超越单通道限制的后向散射,即超级后向散射。
理论
在本研究中,具有旋转对称性的二维散射器的情况被调查分析 ( Jackson, 1999)。当一 $H$ 偏振平面波(仅磁场沿 $z$ 方向)以角频率 $\omega$ 作用于原点处的障碍物时,空气区域中的总磁场可以用极坐标 $(r, \varphi)$ 表示为 ( Ruan, et al., 2010; Ye, et al., 2022)
$$ H_z = H_0\sum_{m}\left[\mathrm{i}^m \mathrm{J}_m(kr) +\mathrm{i}^mS_m\mathrm{H}^{(1)}_m(kr)\right]\mathrm{e}^{\mathrm i m \varphi},\tag{1} $$其中时间依赖性为 $\exp(-\mathrm i \omega t)$。上述公式的第一项代表入射场,$k$ 为空气中的波数。这里 $\mathrm{J}_m(kr)$ 是第一类 $m$ 阶贝塞尔函数,$\mathrm{H}^{(1)}_m(kr)$ 是第一类 $m$ 阶汉克尔函数,散射系数 $S_m$ 对应于第 $m$ 个角动量通道中的散射场强度。$H_0$ 为入射波的振幅。
$$ H_z = H_0\sum_{m}\left[\frac{\mathrm{i}^m}{2}\mathrm{H}^{(2)}_m(kr)+\frac{1+2S_m}{2}\mathrm{i}^m\mathrm{H}^{(1)}_m(kr)\right]\mathrm{e}^{\mathrm i m \varphi}.\tag{2} $$注:入射波在第 $m$ 通道中由 $\frac {\mathrm i^m} {2}\mathrm{H}^{(2)}_m(kr)$ 表示,而出射波变为 $\frac{1+2S_m}{2}\mathrm i^m\mathrm{H}^{(1)}_m(kr)$。因此,$S_m$ 的取值范围受限于能量守恒和角动量守恒,即 $\left|\frac{1+2S_m}{2}\right| \leq \left|\frac {1} {2}\right|$(如 图 1 所示)。等号成立时材料无损耗。
对于此类散射体,总的散射截面可以表达为 $S_m$ 的函数:
$$Q_{\mathrm{sc}}=\frac{2\lambda}{\pi}\sum_{m}\vert S_m\vert^2,\tag{3}$$当第 $m$ 通道中 $S_m=-1$ 时,散射截面最大。实际上可以验证这对应于该系统的束缚态。此外,差分散射截面为:
$$ \sigma(\varphi)=\frac{\lambda}{2\pi}\lim_{r\rightarrow \infty}kr\left|\sum_{m}\mathrm{i}^mS_m\mathrm{H}^{(1)}_m(kr)\mathrm{e}^{\mathrm i m \varphi}\right|^2,\tag{4} $$其中 $\sigma(0)$ 和 $\sigma(\pi)$ 分别对应于前向和后向散射。使用熟知的渐进行为公式 $\mathrm{H}_m^{(1)}(x)\sim \sqrt{\frac{2}{\pi x}}\mathrm e^{\mathrm i(x-m\pi/2-\pi/4)}$ 当 $ x \rightarrow \infty $ 时,$\sigma (\varphi)$ 变为
$$ \sigma(\varphi)=\frac{\lambda}{\pi^2}\left|\sum_{m}S_m\mathrm{e}^{\mathrm i m \varphi}\right|^2.\tag{5} $$一般来说,在亚波长对象中,没有共振的角动量通道对散射截面的实际贡献非常小。此外,虽然对于 $m=1$,偶极矩更易于在外场下产生,但高阶共振模式仅表现出显著狭窄的线宽。因此,只有在亚波长系统中 $S_m=-1$ 才会在共振时出现,在偏离共振时 $S_m$ 快速接近零并且对 $\sigma(\varphi)$ 贡献微乎其微。所以方程式 (5) 可简化为 $\sigma(0)\approx\frac{\lambda}{\pi^2}\sum_{n}1$ 和 $\sigma(\pi)\approx\frac{\lambda}{\pi^2}\left|\sum_{n}(-1)^{n}\right|^2$ 对于前向和后向散射分别成立,其中 $n$ 仅取共振模式。进一步指出,对于亚波长超散射体,总散射截面可以通过前向散射进行估算: $Q_{\mathrm{sc}}\approx2\sqrt{\lambda\sigma(0)} $,表明正相关存在。因此,在不同共振模式结合时,前向散射总是被增强,而两个相邻通道的后向散射互相抵消。这就再次验证了通过连续角动量模叠加构建的超散射体具有微不足道的后向散射特性。另一方面,奇(偶)数 $m$ 的模态组合可以通过后向散射截面正比于参与模式数量平方的方式实现增强。这种方法使得可以显著增强后向散射而不会改变前向和总散射截面。
实际上,方程式 (5) 确实是傅里叶级数的形式,并且其系数值由能量和角动量守恒所限制。传统的超散射研究通过在连续角动量通道中构造共振来增加总散射截面,从而导致散射角度分布接近达耳他函数形式 $\delta(\varphi)$。这解释了图 2(a) 中超散射体消失后向散射的现象。而后向散射的成分则来自于位移后的达耳他函数 $\delta(\varphi-\pi)$,可以视为 $\sum_{m}\mathrm{e}^{\mathrm -\mathrm i m \pi }\mathrm{e}^{\mathrm i m \varphi }$ 的极限。这种序列的散射系数给出了强烈后向散射如图 2(b) 所示,但物理上不可能。为了符合散射系数范围,该序列 $\mathrm{e}^{\mathrm -\mathrm i m \pi }$ 被平移和缩放,使其在复平面内形成一个圆圈 $S_m = \frac 12\mathrm{e}^{\mathrm -\mathrm i m \pi }-\frac 12$。从而使得在有限角动量通道中获得了最大后向散射(图 2(c))。请注意,这与先前推导的散射系数一致,并为有限共振角动量通道提供了最大后向散射。散射系数的最后一项来自复平面上的平移,贡献一个前向散射截面可与后向散射相比拟。因此,在超散射体之间存在后向与前向散射截面之间的权衡。
模型和结果
由于高角动量通道中共振模式倾向于获得更高的固有频率,在非相邻模态的结合时避免重叠中间模式是超级后向散射的一个难点。 这里,我们引入一个最小模型来说明如何最大化后向散射。结构如图 3 所示,它是一个半径为 $a$ 的等离子体纳米棒,并且该纳米棒由阻抗量化的感应超表面覆盖。这里的等离子体材料的相对介电常数通过德鲁德模型描述为 $\varepsilon_\mathrm p =(1-\omega_\mathrm p^2/\omega^2)$,其中 $\omega_\mathrm p$ 为等离子频率。边界条件因此修改如下:
$$ H_z(r)\vert_{r=a^+}-H_z(r)\vert_{r=a^-}=-\frac{E_\varphi(r)}{Z_\mathrm s}\vert_{r=a^+},\tag{6} $$ $$ E_\varphi(r)\vert_{r=a^+}=E_\varphi(r)\vert_{r=a^-}.\tag{7} $$实际上,散射体的束缚态来源于表面等离子波 ( Ye, et al., 2023)。因此,界面阻抗改变了表面波的能量-动量色散,并从而改变共振频率。为了说明这种相关性,在图 4 中展示了覆盖超表面的等离子体纳米棒的修改表面波色散关系(蓝色实线)和相应的结构共振(红色点表示频率,深蓝色条形表示 linewidth)。其中选择的等离子频率为 $\omega_\mathrm p =0.5c/a$。在这里 $k_\parallel$ 是界面处的表面波沿行波常数。可以看到,共振频率恰好是光子带隙中的 $k_\parallel$ 与 $a^{-1}$ 的整数倍相重合。作为对比,也可以在图 4 中看到未覆盖超表面时纯等离子体空气界面的主色散关系(橙色虚线)。可以证明,在表面阻抗 $\mathrm{Im}(Z_\mathrm s)>0$ 下,高横向波数处的等离子体表面波频率被抑制,导致重叠共振峰,这也是薄介电层覆盖时的情况。
图 4(b) 中也显示了极窄的线宽,这表明 $|S_m|^2$ 随频率变化的不同 $m$ 值而变化,确保了远离共振的角动量通道贡献可忽略不计。在这个模型中,在不同角动量通道中的共振模式表现出不同的径向分布。更高阶模式由于在界面处更强的局域化而导致更显著的扰动和频率降低。这导致建立了非单调表面波色散关系,从而使得可以实现非相邻模态叠加而不经历中间模态干扰。
为了进一步演示后向散射与模式叠加之间的相互作用,我们通过改变不同的表面阻抗构建了两个散射器。图 4(a) 中的散射体设置了 $Z_\mathrm s =102\,\mathrm i Z_0$ 作为表面阻抗,在该设置下在 $\omega=0.34492\,c/a$ 处通过 $m=\pm1, \pm2, \pm3$ 模式叠加实现了超散射。相比之下,图 4(c) 中显示了在约 $\omega=0.35076\,c/a$ 的频率处,表面阻抗调谐为 $Z_\mathrm s =533.5\,\mathrm i Z_0$ 时由 $m=\pm1, \pm3, \pm5$ 模态叠加实现的超散射。这两种不同散射体的远场散射图案如图 5 所示。这两个超散射体的总散射截面相似,但在后向散射方面有很大的不同。虽然由于偶极模式和其他模式之间的轻微偏差(如 图3(b) 和 3(d) 中所展示),其散射截面没有达到理想情况,上述模态叠加对后向散射的影响依然成立。 在图 5(a), $m=\pm2$ 和 $m=\pm3$ 通道互相抵消前向散射,只剩下 $m=\pm1$ 模式贡献,使得 $\sigma(0)$ 大约为 $4\lambda/\pi^2$。对于奇模叠加的情况(图 5(b)),正如预期的一样,观察到后向散射与前向散射一样被增强,表明实现了超级后向散射。在这种情况下,后向散射达到单一通道限制的 29.43 倍(理想情况下最多可达 36 倍),是普通超散射器最强后向散射的 7.35 倍。 此外我们计算得到 图 5(a) 的 $Q_\mathrm{sc}=5.60(2\lambda/\pi)\approx2\sqrt{\lambda \sigma(0)}=5.63(2\lambda/\pi)$ 和 图 5(b) 的 $Q_\mathrm{sc}=5.34(2\lambda/\pi)\approx2\sqrt{\lambda \sigma(0)}=5.42(2\lambda/\pi)$,验证了总散射截面与前向散射截面之间的关联。
实际上,没有任何理论限制阻止进一步将模式进行超叠加以持续改善反射率。对于多通道共振退化散射体而言,各个模态的径向场分布是不同的。因此,通过设计径向材料参数分布的不同方式可以对不同模态产生差异化的扰动,从而实现特定模态组合的设计。然而,参数微调的敏感性和损耗可能使得难以组装高退化模式的散射器。因此,探索使用低损耗人工材料如伪表面等离子体 ( Wu, et al., 2019; Shcherbinin, et al., 2020)、额外共振机制如声子极化子 ( Chern, et al., 2006) 和各向异性材料如双曲介质将是在超散射方面未来的研究方向 ( Kumar, et al., 2020; Qian, et al., 2018)。
近场散射问题的分布提供了一个另外的视角,如图 6 所示。近场区域中的场强分布并不像远场那样表现出相同的散射角度分布特性。典型超散射体通常在结构后方产生一个大的阴影,并且这个阴影远大于颗粒的实际物理大小,与 图6(a) 和 6(b) 中一致。因此,超散射体能够保护它后面的物体免受散射。这归因于前向散射波在散射体数个波长之外同入射平面波相干抵消的事实。然而,前向散射并不贡献电磁波的聚焦能力。通过如图 6(b) 中所示的超级后向散射,反射和入射波都被增强,从而提供了更多的应用潜力。
结论
总之,在亚波长超散射体中,只有支持共振的角动量通道对散射截面有贡献,因此可以分析这样系统的方向性。我们发现前向散射与总散射截面之间存在正相关关系,表明任何共振模式的贡献都会增强前向散射。 相比之下,在相邻角动量通道中的共振模式叠加中后向散射被抵消了。 为克服这一点,我们揭示可以通过人为选择奇(偶)数角动量模态进行超叠加来增加后向散射而不改变总散射截面,从而赋予设计散射特性一个新的自由度。 通过特定设计的非单调表面波色散实现了将不相邻模式组合在一起的显著强后向散射,验证了方法的有效性。此外,可以通过特定设计使得重叠模态数量的平方形式进一步增强。
应该指出的是,还有其他方式实现超散射的工作 ( Shamkhi, et al., 2023; Qian, et al., 2022)。这些探索已经扩展了原始定义的超散射,导致破坏旋转对称性和能量守恒,并可能在某些条件下实现超级后向散射。众所周知,具有特定设计的亚波长天线可以在特定入射方向上表现出强烈的后向散射,但仅适用于扭曲旋转对称性的情况。我们的方法基于严格的分析,同时考虑到角动量和能量守恒,提供了一个各向同性的强后向散射。总的来说,该方法也适用于其他具有旋转对称性的结构。我们的工作不仅为电磁超散射的基本理解提供了更深入的视角,还为纳米尺度的应用控制散射特性提供了一条实际路线。
致谢
本项研究得到了国家自然科学基金资助(NSFC, 项目编号:12205067、12375199 和 12175050)。
参考文献
- Rayleigh (1871)
- Rayleigh, L. (1871). On the light from the sky, its polarization and colour. Phil Mag, 41. 107–120.
- Rayleigh (1871)
- Rayleigh, L. (1871). On the light from the sky, its polarization and colour. Phil Mag, 41. 274–279.
- Jackson (1999)
- Jackson, J. (1999). Classical electrodynamics (3rd ed). Wiley.
- Alfaro-Mozaz, Alonso-González, Vélez, Dolado, Autore, Mastel, Casanova, Hueso, Li, Nikitin & (2017)
- Alfaro-Mozaz, F., Alonso-González, P., Vélez, S., Dolado, I., Autore, M., Mastel, S., Casanova, F., Hueso, L., Li, P., Nikitin, A. & (2017). Nanoimaging of resonating hyperbolic polaritons in linear boron nitride antennas. Nature communications, 8(1). 15624. https://doi.org/10.1038/ncomms15624
- Padilla & Averitt (2022)
- Padilla, W. & Averitt, R. (2022). Imaging with metamaterials. Nature Reviews Physics, 4(2). 85–100. https://doi.org/10.1038/s42254-021-00394-3
- Altug, Oh, Maier & Homola (2022)
- Altug, H., Oh, S., Maier, S. & Homola, J. (2022). Advances and applications of nanophotonic biosensors. Nature nanotechnology, 17(1). 5–16. https://doi.org/10.1038/s41570-022-00368-8
- Aigner, Tittl, Wang, Weber, Kivshar, Maier & Ren (2022)
- Aigner, A., Tittl, A., Wang, J., Weber, T., Kivshar, Y., Maier, S. & Ren, H. (2022). Plasmonic bound states in the continuum to tailor light-matter coupling. Science advances, 8(49). eadd4816. https://doi.org/10.1126/sciadv.add481
- Salihoglu, Shi, Li, Wang, Luo, Bondarev, Biehs & Shen (2023)
- Salihoglu, H., Shi, J., Li, Z., Wang, Z., Luo, X., Bondarev, I., Biehs, S. & Shen, S. (2023). Nonlocal Near-Field Radiative Heat Transfer by Transdimensional Plasmonics. Physical Review Letters, 131(8). 086901. https://doi.org/10.1103/PhysRevLett.131.086901
- Ruan & Fan (2010)
- Ruan, Z. & Fan, S. (2010). Superscattering of light from subwavelength nanostructures. Physical review letters, 105(1). 013901. https://doi.org/10.1103/PhysRevLett.105.013901
- Ruan & Fan (2011)
- Ruan, Z. & Fan, S. (2011). Design of subwavelength superscattering nanospheres. Applied Physics Letters, 98(4).
- Mirzaei, Miroshnichenko, Shadrivov & Kivshar (2014)
- Mirzaei, A., Miroshnichenko, A., Shadrivov, I. & Kivshar, Y. (2014). Superscattering of light optimized by a genetic algorithm. Applied Physics Letters, 105(1).
- Kumar & Kajikawa (2020)
- Kumar, R. & Kajikawa, K. (2020). Superscattering from cylindrical hyperbolic metamaterials in the visible region. Optics Express, 28(2). 1507–1517.
- Qian, Lin, Yang, Xiong, Wang, Li, Kaminer, Zhang & Chen (2019)
- Qian, C., Lin, X., Yang, Y., Xiong, X., Wang, H., Li, E., Kaminer, I., Zhang, B. & Chen, H. (2019). Experimental observation of superscattering. Physical review letters, 122(6). 063901.
- Qian, Lin, Yang, Gao, Shen, Lopez, Kaminer, Zhang, Li, Soljacic & (2018)
- Qian, C., Lin, X., Yang, Y., Gao, F., Shen, Y., Lopez, J., Kaminer, I., Zhang, B., Li, E., Soljacic, M. & (2018). Multifrequency superscattering from subwavelength hyperbolic structures. Acs Photonics, 5(4). 1506–1511.
- Qin, Qian, Shen, Wang, Kaminer, Chen & Wang (2023)
- Qin, Z., Qian, C., Shen, L., Wang, X., Kaminer, I., Chen, H. & Wang, H. (2023). Superscattering of water waves. National Science Review, 10(7). nwac255.
- Liberal, Ederra, Gonzalo & Ziolkowski (2015)
- Liberal, I., Ederra, I., Gonzalo, R. & Ziolkowski, R. (2015). Superbackscattering from single dielectric particles. Journal of Optics, 17(7). 072001.
- Powell, Mrnka, Hibbins & Sambles (2022)
- Powell, A., Mrnka, M., Hibbins, A. & Sambles, J. (2022). Superscattering and directive antennas via mode superposition in subwavelength core-shell meta-atoms. Photonics, 9(1). 6.
- Powell, Hibbins & Sambles (2021)
- Powell, A., Hibbins, A. & Sambles, J. (2021). Multiband superbackscattering via mode superposition in a single dielectric particle. Applied Physics Letters, 118(25).
- Ye, Wang, Yao, Wang, Yuan & Zhou (2023)
- Ye, X., Wang, Y., Yao, J., Wang, Y., Yuan, C. & Zhou, Z. (2023). Structure-independent flat bands induced by discontinuity plasma-air interface in photonic crystals. Physical Review B, 107(19). 195301. https://doi.org/10.1103/PhysRevB.107.195301
- Wu, Fang, Quan, Han, Yin, Li & Sheng (2019)
- Wu, H., Fang, Y., Quan, J., Han, Y., Yin, Y., Li, Y. & Sheng, Z. (2019). Multifrequency superscattering with high Q factors from a deep-subwavelength spoof plasmonic structure. Physical Review B, 100(23). 235443.
- Shcherbinin, Fesenko, Tkachova & Tuz (2020)
- Shcherbinin, V., Fesenko, V., Tkachova, T. & Tuz, V. (2020). Superscattering from subwavelength corrugated cylinders. Physical Review Applied, 13(2). 024081.
- Chern, Chang & Chang (2006)
- Chern, R., Chang, C. & Chang, C. (2006). Interfacial operator approach to computing band structures for photonic crystals of polar materials. Physical Review B, 73(23). 235123.
- Shamkhi, Kupriianov, Weiss, Pavlov, Redka, Bobrovs, Kivshar, Shalin & (2023)
- Shamkhi, H., Kupriianov, A., Weiss, T., Pavlov, A., Redka, D., Bobrovs, V., Kivshar, Y., Shalin, A. & (2023). Superscattering emerging from the physics of bound states in the continuum.. Nature Communications, 14(1). 4689–4689.
- Qian, Yang, Hua, Wang, Lin, Cai, Ye, Li, Kaminer & Chen (2022)
- Qian, C., Yang, Y., Hua, Y., Wang, C., Lin, X., Cai, T., Ye, D., Li, E., Kaminer, I. & Chen, H. (2022). Breaking the fundamental scattering limit with gain metasurfaces. Nature communications, 13(1). 4383.
- Lee, Nomura, Schmalenberg, Dede & Iizuka (2019)
- Lee, T., Nomura, T., Schmalenberg, P., Dede, E. & Iizuka, H. (2019). Directional Acoustic Superscattering by Coupled Resonators. Phys. Rev. Appl., 12(5). 054059. https://doi.org/10.1103/PhysRevApplied.12.054059
- Ye, Wang, Yao, Yuan, Zhou, Astafiev & Kudryavtsev (2022)
- Ye, X., Wang, Y., Yao, J., Yuan, C., Zhou, Z., Astafiev, A. & Kudryavtsev, A. (2022). Radiation pattern in a tunable plasma window antenna. Journal of Physics D: Applied Physics, 55(34). 345201. https://doi.org/10.1088/1361-6463/ac7364
- Díaz-Rubio, Asadchy, Elsakka & Tretyakov (2017)
- Díaz-Rubio, A., Asadchy, V., Elsakka, A. & Tretyakov, S. (2017). From the generalized reflection law to the realization of perfect anomalous reflectors. Science Advances, 3(8). e1602714. https://doi.org/10.1126/sciadv.1602714
- Arbabi, Arbabi, Horie, Kamali & Faraon (2017)
- Arbabi, A., Arbabi, E., Horie, Y., Kamali, S. & Faraon, A. (2017). Planar metasurface retroreflector. Nature Photonics, 11(7). 415+. https://doi.org/10.1038/NPHOTON.2017.96
- Wang, Chen & Sato (2021)
- Wang, S., Chen, K. & Sato, M. (2021). Performance of SAR Polarimetric Calibration Using Hybrid Corner Reflectors: Numerical Simulations and Experimental Measurements. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 14. 440–451. https://doi.org/10.1109/JSTARS.2020.3036392
- Hao, Wang, Yang & Gao (2023)
- Hao, J., Wang, X., Yang, S. & Gao, H. (2023). Intelligent Simulation Technology Based on RCS Imaging. Applied Sciences, 13(18). https://doi.org/10.3390/app131810119
- Feng, Li, Zhang, Han, Wang, Ma & Qu (2018)
- Feng, M., Li, Y., Zhang, J., Han, Y., Wang, J., Ma, H. & Qu, S. (2018). Wide-angle flat metasurface corner reflector. Applied Physics Letters, 113(14). 143504. https://doi.org/10.1063/1.5039403