Which beam get further inside the human body?

This is one of my answers in the Physics Stack Exchange¹. In this answer, I reviewed the different physical processes that occur as high-energy rays travel through matter. It is interesting to see that these differences depending on the energy.

Origin question

If we have a beam of photons and a beam of protons with the same energy, which one will get further inside the human body?²

If we have a beam of photons (high energy X-ray) and a beam of protons both with the same energy, which one will get further inside the human body and why? Can this be explaind due to LET (Linear energy transfer)?

My answer

I suppose that the photon beam you say is the high-energy $\gamma$ -ray produced during nuclear decay, it is ture to say that the photon beam usually travels further. However, the penetrates depth of different beam depends on their energy and medium they interact with.

However, not strictly speaking, protons, due to their charge, can easily interact with atoms in the medium and lose energy, thus having a very short penetration depth. $\gamma$-ray interacts much less with the medium and travels further.

As I mentioned earlier, this process depends on the energy of the beam and the medium in which it interacts with. So not comparing them under a specific energy scale is actually very uncritical. The high-energy particles I am considering here commonly come from nuclear decay, nuclear reactor, and compact accelerators (such as medical equipment), beam can possesses energies of ~MeV. I will give a few examples:

${}^{60}\mathrm{Co}$ can undergo a $\beta$ decay to the excited state of ${}^{60}\mathrm{Ni}$, releasing a electron with a energy of 0.309 MeV. The excited ${}^{60}\mathrm{Ni}$ then emits two photons, each with energies of 1.17 MeV and 1.33 MeV, before transitioning back to its ground state.

Reactions occurring in nuclear fusion： $$ {}^{2}\mathrm{H}+{}^{2}\mathrm{H}\rightarrow {}^{3}\mathrm{He}+n+\text{3.25 MeV} \\\\ {}^{2}\mathrm{H}+{}^{2}\mathrm{H}\rightarrow {}^{3}\mathrm{H}+p+\text{4.0 MeV} \\\\ {}^{2}\mathrm{H}+{}^{3}\mathrm{H}\rightarrow {}^{4}\mathrm{He}+n+\text{17.6 MeV} \\\\ {}^{2}\mathrm{H}+{}^{3}\mathrm{He}\rightarrow {}^{4}\mathrm{He}+p+\text{18.3 MeV} $$

In proton radiation therapy, the energy of protons is set from tens of MeV to hundreds of MeV (Charged particles in radiation oncology ).

At such an energy scale, these high-energy particles can be classified into three categories as follow, each with different mechanisms of interaction with matter：

1. Charged Particles

Protons, electrons, muons and $\alpha$-particles (${}^{4}\text{He}$) all belong to this category.

Charged particles with high kinetic energy can interact with matter by engaging their electric fields with orbital electrons, thereby transferring energy to the electrons. This may cause ionization or excitation of the material. This process is known as Coulomb collision, and the resulting energy loss is referred to as ionization loss. An intuitive conclusion is that the longer the interaction time with the electric field of electrons, the greater the impulse obtained by charged particles, resulting in more energy loss. Hence, slower-moving particles experience substantial ionization losses. The ionization energy loss rate (also known as ionization stopping power) can be roughly written as:

$$\frac 1N \left(\frac{\mathrm dE}{\mathrm dx}\right)_{\text{col}}\propto \frac{nz^2Z}{(v/c)^2},$$

where $E$ is the energy of the particle, $Z$ is the atomic number of the material, $N$ is the number of atoms per unit volume in the medium， $z$ is the charge of the particle in untis of electron charge, $V$ and $c$ are the velocities of charged particles and the speed of light, respectively.

We can conclude that:
(1) The more charges particles carry, the greater the ionization loss.
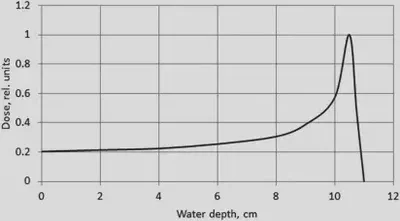
(2) Ionization loss is not directly related to mass, instead it is inversely proportional to the square of the velocity of motion. But if two particles have the same energy, the heavier particle deposits more dose due to its slower speed. Due to this energy correlation, the energy deposition curve of charged heavy ions usually exhibits a so-called Bragg peak. Maximum deposition dose when particles are close to stopping. The follow figure shows the distribution of the absorbed dose along the range of protons with the energy 121 MeV in water (Phys. Med. Biol. 56 (2011) 7725–7735).
(3) Ionization loss strongly depends on the materials interacting with it.

Another mechanism for the deposition of energy by charged particles is referred to bremsstrahlung. When charged particles collide with electrons and atomic nuclei in the medium, acceleration is generated, which transfers a portion of energy to electromagnetic radiation and leads to radiation loss. The stopping power related to the bremsstrahlung is called radiation stopping power, which is proportional to $\frac{(Zz)^2}{m^2}$. Due to the greater the mass, the smaller the impact, the radiation loss is usually only important for electrons.

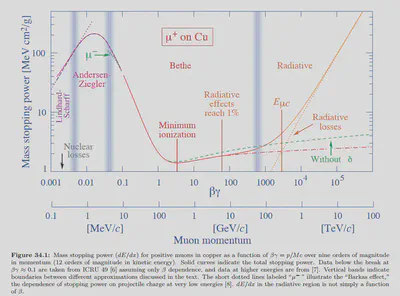
To further illustrate, I cite some data and plots from newest Review of Particle Physics. This figure shows mass stopping power for positive muons in copper as a function of their energy. It can be seen that only a very high energy portion of radiation loss is important.

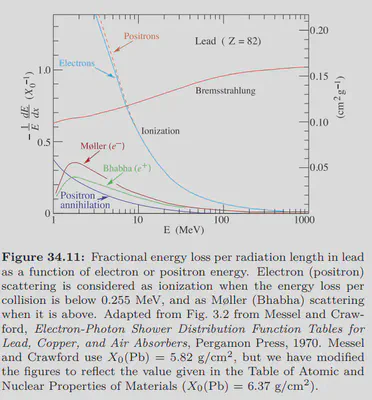
This figure shows fractional energy loss per radiation length in lead as a function of electron or positron energy. It can be seen that ionization loss is reduced in the high-energy region, and radiation loss becomes dominant for electrons. However, in the lower energy part, ionization loss is the main factor, and in materials, the ionization loss of protons is higher than that of electrons. However, such performance heavily relies on materials. The critical energy $E_c$ is sometimes defined as the energy at which the ionization loss and the radiation loss are equal. The critical energy for lead, aluminum, water, and air are 7.43 MeV, 42.70 MeV, 78.33 MeV and 87.92 MeV respectively. If the energy is far below this critical value, the radiation loss becomes negligible, and it can be inferred that electrons travel further than protons due to lower ionization loss. You can find further data at Atomic and Nuclear Properties of Materials.

2. Neutron

Above, we compared the penetration depth of protons and neutrons, and the transport process of neutrons in matter also strictly depends on their energy. Thermal neutron referred to as a free neutron that has kinetic energy of about 0.025 eV, which is approximately the kinetic energy possessed by neutron thermal motion at room temperature. On the other hand, a fast neutron has an energy range of $5\times 10^5\mathrm {eV} \sim 10^7\mathrm{eV}$. Neutrons, having no electric charge, engage matter primarily via nuclear forces (mainly strong interactions). Due to the short-range nature of strong interaction forces and the fact that the nucleus occupies the entire volume of an atom, the interaction between neutrons and matter is weaker than that of protons. Here are several different reactions when neutrons pass through a medium:

Elastic Scattering

When a neutron with energy $E_1$ collides positively with a stationary particle with a mass $M$ times that of a neutron, the energy $E_2$ after the collision satisfies:

$$\frac{E_2}{E_1}=\frac{M-1}{M+1}.$$

Therefore, hydrogen-containing substances and lighter elements have a better slowing effect on fast neutrons. Water, polyethylene, paraffin, graphite, and lithium hydride are common fast neutron moderators, with water and graphite often used in nuclear reactors.

Inelastic Scattering

Neutrons with relatively high energy interact with the target nucleus, causing it to excite and transfer energy to matter. Inelastic scattering can only occur when the energy of neutrons exceeds the first excitation energy of the target nucleus. The first excitation energy of heavy nuclei is usually 100 keV, while the excitation energy of light nuclei is usually several MeV. Therefore, higher energy neutrons are prone to slow down due to inelastic collisions with heavier atomic nuclei with higher atomic numbers.

Radiative capture

$\propto \frac {1}{\sqrt E}$, it is the main reaction that occurs when fast neutrons are absorbed by matter.

3. Photon

The more low-energy electromagnetic waves should be analysed for their specific frequency bands. For instance, as an illustration, another response I provided might helpful Why does Near Infrared (NIR) light allow deeper imaging in biological tissue in Multiphoton Microscopy?.

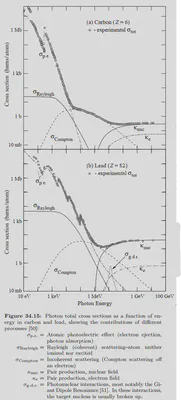
For $\gamma$-ray and X-ray, the primary processes are Compton scattering, photoelecric effect and electron pair effect. There will also be some non-dominant contributions from coherent scattering and photonuclear reactions. Here, I cite scattering cross-sections of various processes involving the interaction between photons of different energies and matter (from Particle Physics Review), note that the vertical axis in the figure is a logarithmic coordinate system.

Finally we come to the comparison of which goes further in matter (described in the new title as in the body). You can see that the answer actually depends on the energy of the beam and the substances with which it interacts. But under these narrower conditions: beams with ~MeV of energy travelling through the body (water), my answer is photons. The proton will quickly decelerate to an energy low enough that violent ionisation loss occurs, depositing almost all of the energy in the body and getting a Bragg peak. Photon beams and proton beams are like two types of bullets, one with greater penetration and one with greater stopping power, and I’ll show you how to take advantage of that property.

Radiotherapy is one of the most common and effective therapies for cancer, which uses high-energy beams to focus on tumors and directly kill cancer cells Radiotherapy should have low toxicity in the entrance channel (normal tissue) and be very effective in cell killing in the target region (tumour). See Physics and biomedical challenges of cancer therapy with accelerated heavy ions and charged particles in radiation oncology.

People found that high‑energy charged particles could be used for cancer treatment, owing to their advantages compared with traditional X‑rays treatment (photon beam). By contrast with X-rays or $\gamma$-rays, which are absorbed by the body and show an exponential decrease in the radiation dose with increasing tissue depth, charged particles deposit little energy at the body’s surface, when their velocity is high, and instead deposit most of their energy just before they come to rest in tissue (corresponding to the Bragg peak, see blow figure)

---

Essentially, $\gamma$-rays propagate farther than charged particles due to their smaller energy loss during their passage, but this depends on the different physical processes behind them. For protons or other charged particles, the stopping power is an energy dependent value that is almost inversely proportional to the square of velocity. Therefore, at the end of the range, a very large dose deposition occurs due to the decrease in energy. For $\gamma$-rays, the photoelectric effect and electron pair effect do not change the energy of photons, but only reduce the number of photons. Therefore, the depth-dose distributions curve of $\gamma$-rays is much smoother. In particular, $\gamma$-rays have no concept of range, which means that there is almost no transmission after this distance, so that photons can almost always reach even very deep places in small quantities.